Ratkaise Kakuro-pulmia

Tässä oppaassa tarjoamme erilaisia käytännön vinkkejä Kakuro-pulmien ratkaisemiseen, joiden vaikeustasot vaihtelevat aloittelijasta asiantuntijatasolle.

Säännöt lyhyesti: Kakuro on ristisanatehtäväpeli, jossa numeroita käytetään laskemaan yhteen laudan 'määritelmäruuduissa' määritettyjä arvoja. Lisäksi jokaisessa summaryhmässä jokainen numero voi esiintyä korkeintaan kerran.

Perinteinen tapa ratkaista Kakuro-pulma on inkrementaalinen: käyttämällä pelilaudalla olevaa tietoa voit varmasti löytää tietyn ruudun arvon, joka voi ottaa vain yhden mahdollisen arvon. Sitten kyseinen arvo täytetään ja prosessi toistetaan, kunnes kaikki pelilaudan ruudut on löydetty.

Joissakin tilanteissa ei ole olemassa tiettyä pelilaudan ruutua, jossa olisi vain yksi mahdollisuus. Näissä tapauksissa kutakin mahdollisuutta on tutkittava erikseen ja poistettava ristiriitojen avulla, kunnes jäljelle jää vain yksi toimintatapa.

Esittelemme alla useita menetelmiä varsinaisen pulman ratkaisemisen edistämiseksi.

Yksilölliset summat tietyille määritelmille

On olemassa määritelmiä, jotka voidaan ratkaista vain tietyllä tavalla:

Summa 3 (kahden solun yli) on aina 1 + 2.
Summa 4 (kahden solun yli) on aina 1 + 3.
Summa 17 (kahden solun yli) on aina 8 + 9.
Summa 6 (kolmen solun yli) on aina 1 + 2 + 3.
Summa 24 (kolmen solun yli) on aina 7 + 8 + 9.

ja niin edelleen... Yleensä voit viedä hiiren osoittimen Kakuro-ruudukon määritelmänumeron päälle, jolloin näkyviin tulee työkaluvihje, joka sisältää kaikki mahdollisuudet kirjoittaa kyseinen summa käyttämällä yksilöllisiä numeroita käytettävissä olevien solujen lukumäärässä.

Yksilöllisellä tavalla kirjoitettavat summat ovat yleensä pieniä tai suuria summia, jotka pakottavat vastaukseen pieniä/suuria numeroita niiden saavuttamiseksi.

Ainutlaatuinen tapa kirjoittaa summa auttaa, mutta pidä mielessä, että kaikki permutaatiot ovat päteviä ja sinun on silti selvitettävä, mitä permutaatiota taululla käytetään.

Rivi-/sarakerajoitukset

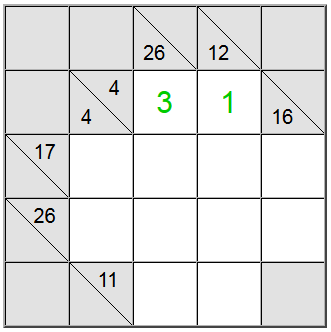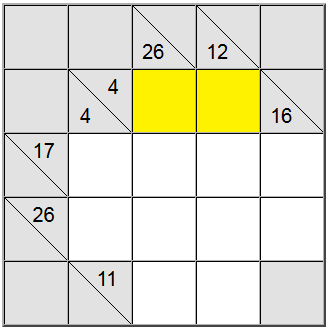
Yllä korostettujen keltaisten solujen summa voidaan kirjoittaa vain yhdellä tavalla: 4 = 1 + 3. Meidän on kuitenkin vielä selvitettävä, mitä permutaatiota (1 + 3 tai 3 + 1) käytetään.

Käy ilmi, että 26:n vertikaalinen määritelmä auttaa meitä: neljän solun summa, joka sisältäisi numeron 1, olisi enintään 1 + 9 + 8 + 7 = 25. Koska summamme on 26, käy ilmi, että numero 1 ei voi olla osa summaa. Siksi keltaisten neliöiden ainoa jäljellä oleva kertaluku on 3 + 1.

Määritelmien leikkauspisteet

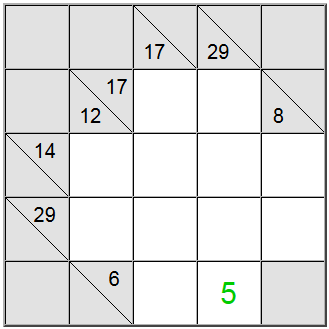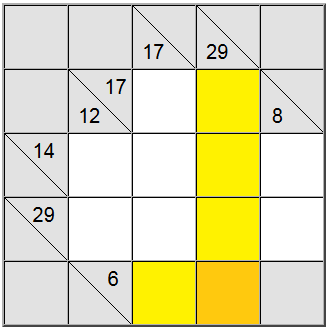
Yllä olevalla taululla vaakasuorat keltaiset neliöt voidaan kirjoittaa muodossa 6 = 1 + 5 tai 6 = 2 + 4. Pystysuora keltainen summa voidaan kirjoittaa vain muodossa 29 = 5 + 7 + 8 + 9.

Näiden kahden summamääritelmän leikkauspisteessä olevan keltaisen neliön on sisällettävä sama numero, joten vaaka- ja pystysuuntaisissa määritelmissä on oltava yhteinen numero, jotta ne voidaan jakaa niiden kesken. Tarkastelemalla yllä olevia mahdollisuuksia voimme helposti päätellä, että 5 on ainoa numero, joka täyttää tämän kriteerin.

Tämä tekniikka toimii erityisen hyvin leikattaessa matalan ja korkean summan määritelmiä. Matala- ja korkean summan määritelmillä on suhteellisen matala tai korkea summan määrittelynumero (esimerkissämme 6 ja 29) verrattuna käytettävissä olevien solujen määrään. Koska 6 on suhteellisen matala, se pakottaa matalat numerot summaesityksessä, ja 29 pakottaa korkeat numerot (jotta nämä summat saavutetaan annetulla solumäärällä). Siksi matalan ja korkean numeron leikkauspisteessä on todennäköisesti vain yksi ehdokas solun varsinaiselle arvolle.

Summaryhmän min-/max-arvot

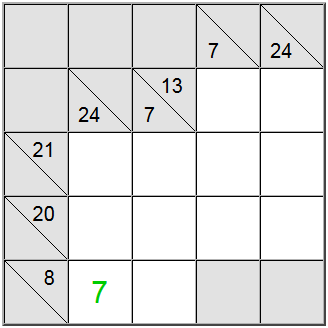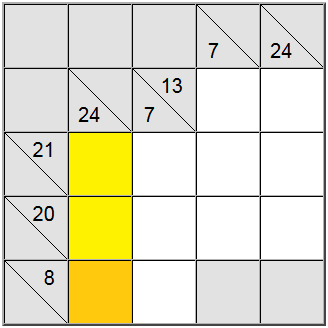
Joskus on hyödyllistä selvittää summaryhmän maksimi- tai minimiarvo. Tämä voi antaa käsityksen siitä, mikä on kyseisen summan kelvollinen numeroalue, mikä puolestaan auttaa sinua tekemään korrelaatioita muiden rajoitusten kanssa ja selvittämään taululla olevat yksilölliset sijoitukset.

Yllä olevassa esimerkissä keltaiset pystysuorat solut hyväksyvät vain arvoja, jotka ovat 7 tai suurempia. Jos yrität antaa luvun 6, voit helposti päätellä, että 6 + 9 + 8 = 23, joten määritelmän summaa 24 ei voida saavuttaa.

Koska 7 on minimi, vaakasuora määritelmä, jossa summa on 8, pakottaa 7:n tähän asentoon.

Johtopäätös

Harjoittelu on paras tapa nähdä, miten tätä neuvoa voidaan soveltaa oikeissa Kakuro-peleissä. Pelaa pulmapeliä oikeasti. Toivotamme sinulle onnea ja paljon hauskaa!

Pelaa Kakuroa